На координатной прямой отмечены точка О — начало отсчета и точки А, В, С, D, Е.
Числу 1,6 на координатной прямой соответствует точка:
На координатной прямой отмечены точка О — начало отсчета и точки А, В, С, D, Е.
Числу 1,6 на координатной прямой соответствует точка:
На рисунке изображена правильная четырехугольная пирамида SABCD, точка O — точка пересечения диагоналей основания ABCD. Среди прямых BC; BD; SO; SB; SD укажите прямую, по которой пересекаются плоскости DSO и SCB.
Среди значений аргумента, равных ![]()
![]()
![]()
![]()
![]() укажите то, при котором значение функции
укажите то, при котором значение функции  равно нулю.
равно нулю.
Укажите номер формулы, по которой можно найти делимое n при делении с остатком, если делитель 15, неполное частное k, остаток 7 (делимое n — натуральное число).

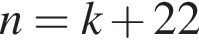
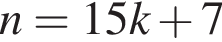
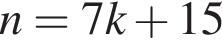
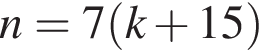
Укажите номер квадратного уравнения, произведение действительных корней которого равно 5.


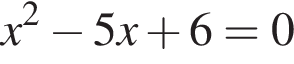
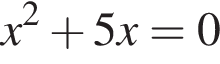

Укажите номера пар, состоящих из промежутков, объединением которых является изображенный на рисунке промежуток.
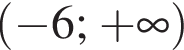 и
и 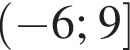
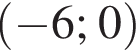 и
и 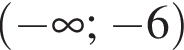 и
и 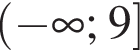
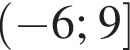 и
и 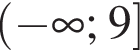 и
и 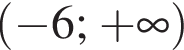
Толя купил 3 альбома и 5 карандашей. Стоимость одного альбома равна 1 р. 20 к., а стоимость одного карандаша равна 25 к. Какая сумма (в копейках) осталась у Толи после покупки альбомов и карандашей, если всего у него было 6 р.?
Найдите значение выражения 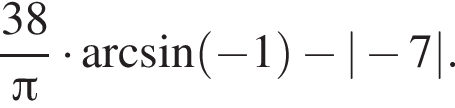
Квадрат, длина диагонали которого равна 8, лежит в плоскости α. Сфера касается плоскости α в точке пересечения диагоналей квадрата. Найдите площадь сферы, если расстояние от центра сферы до вершины квадрата равно ![]()

Укажите номера выражений, которые имеют смысл при 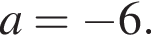
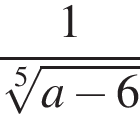
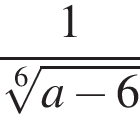
Дана прямая треугольная призма ABCA1B1C1. Точка M является серединой ребра AB,  (см. рис.). Выберите верные утверждения. В ответе укажите номера выбранных утверждений.
(см. рис.). Выберите верные утверждения. В ответе укажите номера выбранных утверждений.
1) Расстояние от точки C1 до прямой AB равно длине отрезка BC1.
2) Расстояние от точки C1 до прямой AB равно длине отрезка C1M.
3) Расстояние от точки A до прямой ВС равно длине отрезка АВ.
4) Расстояние между прямыми ВВ1 и CC1 равно длине отрезка ВС1.
5) Расстояние между прямыми А1В1 и АВ равно длине отрезка AA1.
6) Расстояние от точки В до прямой АС равно длине отрезка ВС.
Функция задана формулой 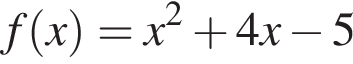 на множестве действительных чисел
на множестве действительных чисел ![]() Для начала каждого из предложений А–В подберите его окончание 1–6 так, чтобы получилось верное утверждение.
Для начала каждого из предложений А–В подберите его окончание 1–6 так, чтобы получилось верное утверждение.
A) Сумма координат точки пересечения графика данной функции с осью ординат равна ...
Б) Сумма нулей данной функции равна ...
В) Наименьшее значение данной функции на области определения равно ...
1) 9
2) −4
3) 5
4) −9
5) −5
6) 4
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Найдите сумму всех натуральных чисел, которые кратны 9 и больше 141, но меньше 170.
Найдите значение выражения ![]() если
если 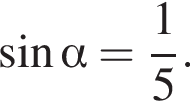
Радиус окружности, описанной около прямоугольного треугольника ABC  равен
равен ![]() Найдите значение выражения
Найдите значение выражения  если
если 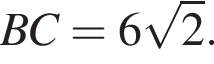
Пятый член геометрической прогрессии равен 48, а шестой ее член равен 96. Найдите сумму четырех первых членов этой прогрессии.
Проездной билет на автобус на месяц стоит 39 р., а стоимость билета на одну поездку на автобусе равна 80 к. Сколько поездок на автобусе совершила Маша за месяц, покупая только билеты на одну поездку, если известно, что 75% от суммы денег, которую она потратила за месяц на оплату поездок на автобусе, равны стоимости проездного билета на автобус на месяц?
Найдите сумму наименьшего и наибольшего целых решений двойного неравенства 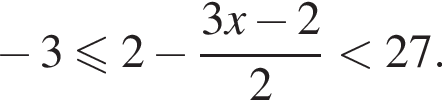
Функция 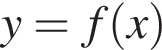 определена на множестве действительных чисел, точки
определена на множестве действительных чисел, точки 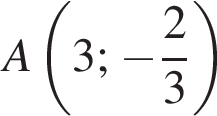 и
и 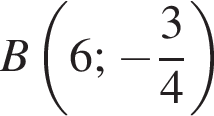 принадлежат графику данной функции. Найдите значение выражения
принадлежат графику данной функции. Найдите значение выражения  если известно, что график функции
если известно, что график функции 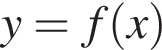 симметричен относительно оси ординат.
симметричен относительно оси ординат.
Радиус окружности, вписанной в правильный шестиугольник, равен ![]() Найдите значение выражения
Найдите значение выражения ![]() где S — площадь правильного шестиугольника.
где S — площадь правильного шестиугольника.
Найдите произведение корней уравнения  В ответ запишите найденное произведение, увеличенное в 11 раз.
В ответ запишите найденное произведение, увеличенное в 11 раз.
Дана правильная несократимая дробь. При делении ее знаменателя на числитель неполное частное равно 8, а остаток равен 3. Если числитель дроби увеличить на 75%, то полученная дробь будет равна ![]() Найдите наименьшее общее кратное числителя и знаменателя исходной дроби.
Найдите наименьшее общее кратное числителя и знаменателя исходной дроби.
Цилиндр пересечен такой плоскостью, параллельной оси цилиндра, что в сечении получился квадрат площадью 100. Найдите значение выражения ![]() где S — площадь боковой поверхности цилиндра, если расстояние от оси цилиндра до плоскости сечения равно
где S — площадь боковой поверхности цилиндра, если расстояние от оси цилиндра до плоскости сечения равно ![]()
Найдите наименьшее целое решение неравенства 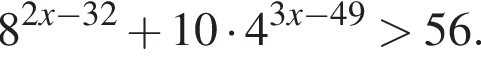
Найдите (в градусах) сумму различных корней уравнения  на промежутке (−150°; −55°).
на промежутке (−150°; −55°).
Найдите произведение наименьшего целого решения решения на наибольшее целое решение неравенства 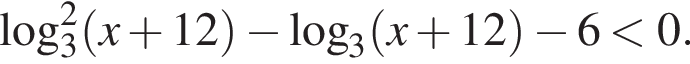
Плоскость, параллельная основанию треугольной пирамиды, делит ее высоту в отношении 5 : 3, если считать от вершины пирамиды. Найдите площадь сечения пирамиды данной плоскостью, если она меньше площади основания пирамиды на 39.
Найдите сумму корней (корень, если он единственный) уравнения 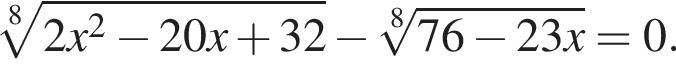 В ответ запишите полученный результат, увеличенный в 6 раз.
В ответ запишите полученный результат, увеличенный в 6 раз.
Дана функция 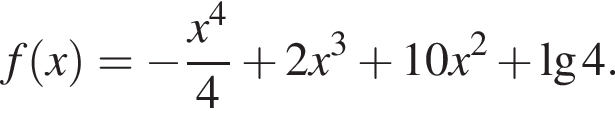 Найдите значение выражения a · n, где a — наибольшее целое отрицательное число из промежутков возрастания данной функции, n — количество всех натуральных чисел из промежутков возрастания данной функции.
Найдите значение выражения a · n, где a — наибольшее целое отрицательное число из промежутков возрастания данной функции, n — количество всех натуральных чисел из промежутков возрастания данной функции.
ABCDA1B1C1D1 — прямой параллелепипед, объем которого равен ![]() Длины сторон AB и BC основания ABCD равны
Длины сторон AB и BC основания ABCD равны ![]() и
и ![]() соответственно, косинус угла ABC равен
соответственно, косинус угла ABC равен 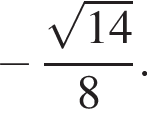 На ребрах AA1 и A1B1 взяты точки M и N соответственно, такие, что AM : MA1 = 4 : 1, A1N : NB1 = 1 : 4. Найдите значение выражения
На ребрах AA1 и A1B1 взяты точки M и N соответственно, такие, что AM : MA1 = 4 : 1, A1N : NB1 = 1 : 4. Найдите значение выражения 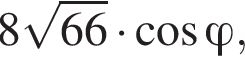 где φ — угол между прямыми MN и BC1.
где φ — угол между прямыми MN и BC1.